Grundlagen: Probabilistik: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
|||
| Zeile 10: | Zeile 10: | ||
== Zielstellung == | |||
Experimentell tätige Wissenschaftler unterliegen dem Zwang, ihre Experimente statistisch auszuwerten. Das dafür erforderliche mathematische Rüstzeug kann in dieser kurzen Einführung in die Probabilistik nicht vermittelt werden. | Experimentell tätige Wissenschaftler unterliegen dem Zwang, ihre Experimente statistisch auszuwerten. Das dafür erforderliche mathematische Rüstzeug kann in dieser kurzen Einführung in die Probabilistik nicht vermittelt werden. | ||
| Zeile 22: | Zeile 22: | ||
Anliegen dieses Kapitels ist die Vermittlung des qualitativen Wissens zu den wahrscheinlichkeitstheoretischen Grundlagen, welche für die qualifizierte Anwendung von Probabilistik-Tools erforderlich ist. | Anliegen dieses Kapitels ist die Vermittlung des qualitativen Wissens zu den wahrscheinlichkeitstheoretischen Grundlagen, welche für die qualifizierte Anwendung von Probabilistik-Tools erforderlich ist. | ||
== Grundbegriffe == | |||
=== Nennwert === | |||
In Anlehnung an den Begriff [http://de.wikipedia.org/wiki/Nennmaß Nennmaß] soll unter Nennwert der geplante Wert für eine physikalisch-technische Größe im weitesten Sinne verstanden werden. Es handelt sich hierbei um einen idealisierten, "exakten Wert", z.B.: | In Anlehnung an den Begriff [http://de.wikipedia.org/wiki/Nennmaß Nennmaß] soll unter Nennwert der geplante Wert für eine physikalisch-technische Größe im weitesten Sinne verstanden werden. Es handelt sich hierbei um einen idealisierten, "exakten Wert", z.B.: | ||
| Zeile 37: | Zeile 37: | ||
<div align="center">[[Datei:Grundlagen_Probabilistik_-_Nennwerte_und_determ-Modell.gif]]</div> | <div align="center">[[Datei:Grundlagen_Probabilistik_-_Nennwerte_und_determ-Modell.gif]]</div> | ||
=== Toleranz === | |||
Ein exakter Nennwert ist praktisch nie realisierbar. Deshalb muss für jeden Nennwert ein Wertebereich (Toleranzfeld) definiert werden, dessen Einhaltung garantiert, dass die Funktionalität der Lösung gewährleistet ist. Diesen zulässigen Wertebereich bezeichnet man auch kurz als Toleranz. Im Spezialfall (z.B. Press-Passungen) liegt der Nennwert außerhalb des Toleranzfeldes. | Ein exakter Nennwert ist praktisch nie realisierbar. Deshalb muss für jeden Nennwert ein Wertebereich (Toleranzfeld) definiert werden, dessen Einhaltung garantiert, dass die Funktionalität der Lösung gewährleistet ist. Diesen zulässigen Wertebereich bezeichnet man auch kurz als Toleranz. Im Spezialfall (z.B. Press-Passungen) liegt der Nennwert außerhalb des Toleranzfeldes. | ||
| Zeile 51: | Zeile 51: | ||
* Für nichtlineare Modelle gilt nicht das [http://de.wikipedia.org/wiki/Superposition_(Mathematik) Superpositionsprinzip]. Deshalb führt die kombinatorische Form der Toleranzanalyse für nichtlineare Probleme nicht mit Sicherheit zu den Extremwerten der Output-Größen '''Y<sub>j</sub>'''. | * Für nichtlineare Modelle gilt nicht das [http://de.wikipedia.org/wiki/Superposition_(Mathematik) Superpositionsprinzip]. Deshalb führt die kombinatorische Form der Toleranzanalyse für nichtlineare Probleme nicht mit Sicherheit zu den Extremwerten der Output-Größen '''Y<sub>j</sub>'''. | ||
=== Streuungen === | |||
Toleranzangaben beziehen sich nur auf die zulässigen Grenzwerte für einen Nennwert. Die tatsächlich auftretenden Istwerte treten je nach Herkunft (z.B. Fertigungsverfahren, Umweltbedingungen, Alterung) innerhalb dieser Grenzwerte mit unterschiedlichen Verteilungsfunktionen auf. In Erweiterung des Toleranz-Begriffes wird für die statistische Analyse von Ausfallwahrscheinlichkeiten der Begriff der "Streuung" benutzt. | Toleranzangaben beziehen sich nur auf die zulässigen Grenzwerte für einen Nennwert. Die tatsächlich auftretenden Istwerte treten je nach Herkunft (z.B. Fertigungsverfahren, Umweltbedingungen, Alterung) innerhalb dieser Grenzwerte mit unterschiedlichen Verteilungsfunktionen auf. In Erweiterung des Toleranz-Begriffes wird für die statistische Analyse von Ausfallwahrscheinlichkeiten der Begriff der "Streuung" benutzt. | ||
| Zeile 64: | Zeile 64: | ||
<div align="center">[[Datei:Grundlagen_Probabilistik_-_Streuungen_und_probabil-Modell.gif]]</div> | <div align="center">[[Datei:Grundlagen_Probabilistik_-_Streuungen_und_probabil-Modell.gif]]</div> | ||
=== Probabilistik === | |||
[http://de.wikipedia.org/wiki/Probabilistik '''Probabilistik'''] (auch als '''Wahrscheinlichkeitstheorie''' bezeichnet) ist aus der Untersuchung von [http://de.wikipedia.org/wiki/Zufall Zufallsgeschehen] hervorgegangen: | [http://de.wikipedia.org/wiki/Probabilistik '''Probabilistik'''] (auch als '''Wahrscheinlichkeitstheorie''' bezeichnet) ist aus der Untersuchung von [http://de.wikipedia.org/wiki/Zufall Zufallsgeschehen] hervorgegangen: | ||
| Zeile 77: | Zeile 77: | ||
== Probabilistische Simulation == | |||
Die Eigenschaften technischer Systeme streuen in der Realität. Sie sind durch ihr Nennverhalten und eine stochastische Verteilung um dieses Nennverhalten gekennzeichnet: | Die Eigenschaften technischer Systeme streuen in der Realität. Sie sind durch ihr Nennverhalten und eine stochastische Verteilung um dieses Nennverhalten gekennzeichnet: | ||
| Zeile 86: | Zeile 86: | ||
=== Statistische Versuchsplanung (Design of Experiments DOE) === | |||
Mittels [http://de.wikipedia.org/wiki/Design_of_Experiments statistischer Versuchsplanung] soll mit möglichst wenigen deterministischen Simulationen der Wirkzusammenhang zwischen Einflussfaktoren (= unabhängige Inputgrößen) und Zielgrößen (= abhängige Outputgrößen) möglichst genau ermittelt werden: | Mittels [http://de.wikipedia.org/wiki/Design_of_Experiments statistischer Versuchsplanung] soll mit möglichst wenigen deterministischen Simulationen der Wirkzusammenhang zwischen Einflussfaktoren (= unabhängige Inputgrößen) und Zielgrößen (= abhängige Outputgrößen) möglichst genau ermittelt werden: | ||
* ... | * ... | ||
Version vom 6. Mai 2014, 11:31 Uhr
Dieses Kapitel wird zur Zeit erarbeitet
Vorläufige Gliederung:
- Zielstellung
- Grundbegriffe
- Probabilistische Simulation
- Probabilistische Analyse
Zielstellung
Experimentell tätige Wissenschaftler unterliegen dem Zwang, ihre Experimente statistisch auszuwerten. Das dafür erforderliche mathematische Rüstzeug kann in dieser kurzen Einführung in die Probabilistik nicht vermittelt werden.
Im Blickfeld dieses Kapitel steht vor allem der Entwicklungsingenieur. Dieser benutzt für seine Berechnungen überwiegend "exakte" Nennwerte. Die Zulässigkeit von Toleranzen ermittelt er danach durch Analyse ihrer Grenzwerte. Damit soll z.B. die Montage oder Funktion auch unter den ungünstigsten Umständen zu 100% sichergestellt werden.
Dem Entwicklungsingenieur ist durchaus bewusst, dass Wahrscheinlichkeiten eine wichtige Rolle beim Auftreten unerwünschter Zustände in seinen Lösungen spielen. Leider sind Menschen (und damit auch Ingenieure) meist sogenannte "Wahrscheinlichkeitsidioten", die das Eintreten bestimmter Ereignisse entweder über- oder unterschätzen (zum "Idiotentest" → Geburtstagsparadoxon).
Der Entwicklungsingenieur hat kaum die Zeit, sich die benötigten mathematischen Methoden tiefgründig anzueignen und sie auf seine Probleme analytisch anzuwenden. Er ist deshalb auf vorhandene Software-Pakete angewiesen, um seine Lösungen einer probabilistischen Analyse zu unterziehen.
Anliegen dieses Kapitels ist die Vermittlung des qualitativen Wissens zu den wahrscheinlichkeitstheoretischen Grundlagen, welche für die qualifizierte Anwendung von Probabilistik-Tools erforderlich ist.
Grundbegriffe
Nennwert
In Anlehnung an den Begriff Nennmaß soll unter Nennwert der geplante Wert für eine physikalisch-technische Größe im weitesten Sinne verstanden werden. Es handelt sich hierbei um einen idealisierten, "exakten Wert", z.B.:
- Physikalische Größe als Produkt aus Maßeinheit und Zahlenwert (Skalar, Vektor, höherstufiger Tensor)
- Geometrisches Element (Punkt, Kurve, Fläche, Körper)
- Funktionale Abhängigkeit (Kennlinie, Kennfeld, Übertragungsfunktion)
Die idealisierten Nennwerte bilden die Grundlage bei der Entwicklung optimaler Lösung für technische Aufgabenstellungen. Dafür gibt es plausible Gründe:
- Physikalische Effekte außerhalb der Quantenmechanik werden mathematisch als Verknüpfung zwischen den aktuellen Istwerten der beteiligten physikalischen Größen beschrieben (Klassische Physik).
- Praktisch sämtliche CAE-Systeme arbeiten mit deterministischen Modellen (basieren auf Effekten der klassischen Physik und euklidischen Geometrie).
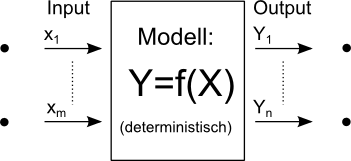
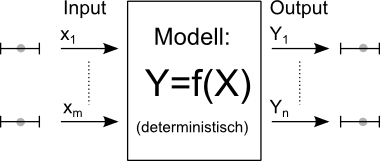
- Deterministische Modelle erzeugen aus "exakten" Eingangsgrößen mittels eindeutiger Übertragungsfunktionen "exakte" Ausgangsgrößen:
Toleranz
Ein exakter Nennwert ist praktisch nie realisierbar. Deshalb muss für jeden Nennwert ein Wertebereich (Toleranzfeld) definiert werden, dessen Einhaltung garantiert, dass die Funktionalität der Lösung gewährleistet ist. Diesen zulässigen Wertebereich bezeichnet man auch kurz als Toleranz. Im Spezialfall (z.B. Press-Passungen) liegt der Nennwert außerhalb des Toleranzfeldes.
Man unterscheidet wie bei den "Nennwerten" unterschiedliche Toleranz-Typen:
- Maßtoleranzen, Bauteil-Toleranzen (z.B. Kennwerte von einfachen elektronischen oder mechanischen Bauelementen)
- Form- und Lagetoleranzen sowie Oberflächenangaben
- Funktionale Toleranzen (Material-Kennlinien, Wandler-Kennfelder, Übertragungsfunktionen)
Handelt es sich um deterministische Modelle mit linearem Übertragungsverhalten, so können durch die Berechnung aller möglichen Kombinationen der Toleranzgrenzen von Xi die Minima/Maxima aller Yj bestimmt werden:
- Ein Beispiel für ein lineares Modell ist die einfache Toleranzkette im OptiYummy-Tutorial.
- Für nichtlineare Modelle gilt nicht das Superpositionsprinzip. Deshalb führt die kombinatorische Form der Toleranzanalyse für nichtlineare Probleme nicht mit Sicherheit zu den Extremwerten der Output-Größen Yj.
Streuungen
Toleranzangaben beziehen sich nur auf die zulässigen Grenzwerte für einen Nennwert. Die tatsächlich auftretenden Istwerte treten je nach Herkunft (z.B. Fertigungsverfahren, Umweltbedingungen, Alterung) innerhalb dieser Grenzwerte mit unterschiedlichen Verteilungsfunktionen auf. In Erweiterung des Toleranz-Begriffes wird für die statistische Analyse von Ausfallwahrscheinlichkeiten der Begriff der "Streuung" benutzt.
Eine Streuung ist definiert durch
- die Toleranz (d.h. die Grenzwerte des Toleranzfeldes) und
- die Verteilungsdichte-Funktion innerhalb des Toleranzfeldes (z.B. Gleich- oder Normalverteilung).
Eine Streuung enthält die Menge aller Werte für die zugehörige streuende Größe:
- deterministische Modelle können jeweils nur ein einzelnes Exemplar (= ein Parametersatz) aus der gesamten Input-Streuung berechnen,
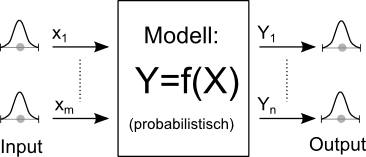
- probabilistische Modelle sind erforderlich, um entsprechend der Verteilungsdichtefunktionen der Input-Streuungen das Verhalten aller möglichen Exemplare zu berechnen (Output-Streuungen):
Probabilistik
Probabilistik (auch als Wahrscheinlichkeitstheorie bezeichnet) ist aus der Untersuchung von Zufallsgeschehen hervorgegangen:
- Die Wahrscheinlichkeitstheorie formalisiert die Modellierung und Simulation von Zufallsereignissen.
- Gemeinsam mit der Statistik, die anhand von Beobachtungen zufälliger Vorgänge Aussagen über das zugrunde liegende Modell trifft, bildet sie das mathematische Teilgebiet der Stochastik.
- Die Stochastik als Lehre von der Häufigkeit und Wahrscheinlichkeit ("Kunst des Vermutens") beschäftigt sich mit der Definition, Durchführung und Auswertung von Zufallsexperimenten.
Zumindest für den Ingenieur ist die Begriffsvielfalt zu den unterschiedlichen Aspekten der Stochastik verwirrend. Folgt man zu diesen Begriffen z.B. den Verlinkungen in der Wikipedia, so gewinnt man leider den Eindruck, dass viele unscharfe Überschneidungen und Querbezüge zwischen diesen Aspekten existieren. Deshalb wird hier eine pragmatische Sicht auf die Entwicklung, Simulation und Analyse probabilistischer Modelle vertreten:
- Es wird bei der Berücksichtigung von Streuungen im Entwicklungsprozess durchgängig der Begriff "Probabilistik" verwendet, obwohl "Stochastik" zutreffender wäre.
- Der Begriff "Stochastik" besitzt ein negatives Image im Sinne von Chaos, Unordnung und Zufall und sollte deshalb im Zusammenhang mit der Entwicklung hochwertiger Produkte vermieden werden.
- Der Begriff "Probabilistik" impliziert dagegen sorgfältiges Arbeiten durch die Berücksichtigung von Wahrscheinlichkeiten (d.h. aller Eventualitäten) im Entwicklungsprozess.
Probabilistische Simulation
Die Eigenschaften technischer Systeme streuen in der Realität. Sie sind durch ihr Nennverhalten und eine stochastische Verteilung um dieses Nennverhalten gekennzeichnet:
- Ursachen für die stochastische Verteilung der Systemeigenschaften sind z.B. Umwelteinflüsse, Fertigungsungenauigkeiten, Prozessunsicherheiten, Alterung und Verschleiß.
- Diese realen Aspekte der Unsicherheit müssen bei der Beurteilung und bei der Auslegung technischer Systeme beachtet werden.
- Mit deterministischer Simulation kann man das vollständige Systemverhalten nicht vorhersagen.
- Erforderlich ist eine probabilistische Simulation. Aus den Streuungen der Eingangsgrößen werden dabei die Streuungen der Ausgangsgrößen berechnet.
Statistische Versuchsplanung (Design of Experiments DOE)
Mittels statistischer Versuchsplanung soll mit möglichst wenigen deterministischen Simulationen der Wirkzusammenhang zwischen Einflussfaktoren (= unabhängige Inputgrößen) und Zielgrößen (= abhängige Outputgrößen) möglichst genau ermittelt werden:
- ...