Grundlagen: Simulation - Solver

Modellberechnung

Simulationen mit numerischen Modellen beruhen im Wesentlichen auf der Berechnung von Modell-Ergebnissen mit Hilfe eines Gleichungslösers (Solver). In diesem Grundlagen-Kapitel liegt der Schwerpunkt auf der Erläuterung der prinzipiellen Wirkungsweise von Solvern zur Simulation dynamischer Systeme im Zeitbereich. Dabei wird beispielhaft Bezug genommen auf die Begriffe und Konzepte, wie sie im Simulationssystem SimulationX verwendet werden.

Numerische Simulation zeitkontinuierlicher Systeme

Kenngrößen eines Simulationslaufes (Zeitachse)

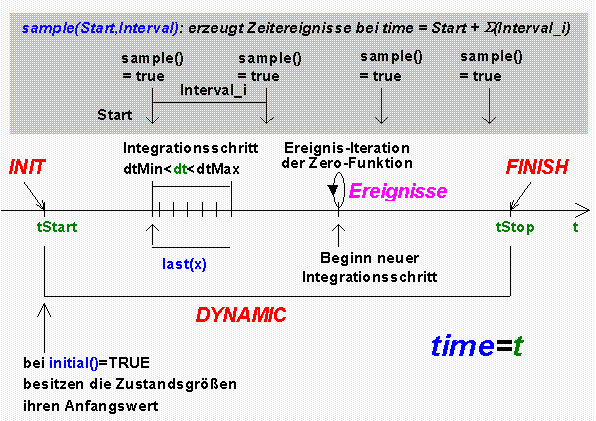
• Aus Sicht des Modells läuft die Simulationszeit time bzw. t in diskreten Schritten dt von tStart bis tStop (meist vorwärts):
  
• Innerhalb des aktuellen Zeitintervalls dt werden in Abhängigkeit vom verwendeten Lösungsverfahren mehrere Stützstellen berechnet:
  • Jede Stützstelle entspricht einer einmaligen Modellberechnung. Demzufolge sind die meisten Modelldurchrechnungen Hilfsrechnungen (mit "unexakten" Werten).
  • Nach Durchführung aller Hilfsrechnungen erfolgt einmalig für das Ende des aktuellen Zeitintervalls dt eine Modellberechnung mit den "richtigen" Modellwerten.
  • Innerhalb des Modell-Algorithmus kann man auf die letzten "richtigen" Modellwerte zugreifen (in SimulationX mit der last-Funktion).
• Bei numerischen Verfahren mit Schrittweitenregelung erfolgt eine automatische Anpassung der Schrittweite dt an die Eigenschaften des Modells zum berechneten Zeitpunkt ("Wie schnell können sich die physikalischen Zustandsgrößen ändern?"):
  • Je empfindlicher Zustandsgrößen des Modells auf andere Modellgrößen reagieren können, desto kleiner wird dt gewählt.
  • Die zulässige Rechenschritte dt kann man begrenzen (dtMin soll "ewiges" Rechnen vermeiden / dtMax soll eckige Signalverläufe vermeiden).
• Die Berechnung mit der sich kontinuierlich anpassenden Schrittweite dt wird gestört durch Ereignis-Zeitpunkte, welche "exakt" angesteuert und berechnet werden müssen. Die Wirkungsweise der erforderliche Ereignisbehandlung wird in einem gesonderten Abschnitt erläutert.

Abschnitte eines Simulationslaufes

Ein Simulationslauf im Zeitintervall tStart ≤ time ≤ tStop besteht aus den Abschnitten INIT, DYNAMIC und FINISH. Im Folgenden wird die Aufgabe dieser Abschnitte zum einen aus numerischer Sicht erläutert. Zum anderen erfolgen Hinweise, welche Aufgaben die zugehörigen Modellabschnitte für die Nutzung von Modellen im Konstruktionsprozess übernehmen:

INIT ( time = tStart )
dient der Ermittlung konsistenter Anfangswerte für alle Zustandsgrößen (Bilder aus der SimulationX-Hilfe):

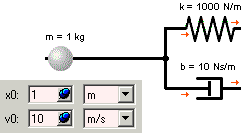
• Die Anfangswerte charakterisieren den (energetischen) Zustand des Modells zu Beginn der Simulation.
• Anfangswerte gewöhnlicher DGL sind immer konsistent (ODE: Ordinary Differential Equation). Der Solver kann daraus eindeutig die Werte der höchsten Ableitungen berechnen (im Beispiel Beschleunigung a(tStart)=-1100 m/s²).
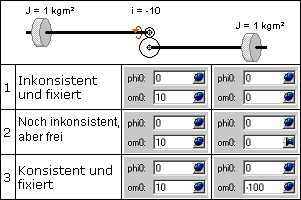
• Modelle mit Zwangsbedingungen (z.B. für Getriebe) führen zu Algebro-Differenzialgleichungen (DAE: Differential Algebraic Equation). Hier können einige Zustandsgrößen nicht unabhängig voneinander gewählt werden:
  
• Man muss sich entscheiden, welche Anfangswerte man definiert vorgibt (fixiert). Die nicht fixierten Anfangswerte versucht der Solver, aus den im Modell in Form von Gleichungen beschriebenen Zwangsbedingungen zu berechnen. Dies gelingt insbesondere bei stark nichtlinearen oder nicht nichteindeutigen Zusammenhängen nicht immer!
• Man sollte möglichst viele gültige Anfangswerte vorgeben und fixieren! Nur dort, wo die analytische Berücksichtigung der Abhängigkeiten praktisch unmöglich ist, überlässt man dem Solver die Anfangswertbestimmung!

===>>> Dieses Kapitel wird zur Zeit erarbeitet !!! <<<===

Vorläufige weitere Gliederung:

• Ableitungs- und Integralform von DGL
• Wechselwirkung von Zustandsgröße Y(t) und Ableitung YP(t)
• Zentraler "Integrationskern" (Solver)
• Prinzip der numerischen Integration
• Explizite und implizite Verfahren
• Einschritt- und Mehrschritt-Verfahren
• Explizite Einschrittverfahren (Beispiele)
• Implizite Verfahren (Prinzip)
• Implizite Verfahren (Prädiktor-Korrektor-Verfahren)
• Qualitäten von Integrationsverfahren
• Konfiguration des Solvers

Zeitdiskrete Ereignisse

• Ereignisse im Simulationslauf
• Numerische Definition von Ereignissen
• Klassifizierung numerischer Ereignisse
• Ereignisbehandlung (SimulationX)
• Beispiel: Extremwert-"Sensoren" (SimulationX)

Lineare und nichtlineare Systeme

• Modellcharakter von Systemen
• Dynamische Systeme
• Wann kann man ein System als Linear behandeln?
• Wann muss man ein System als Nichtlinear behandeln?