Software: FEM - Tutorial - Elektrostatik - MP - Modellbildung: Unterschied zwischen den Versionen
Aus OptiYummy
Zur Navigation springenZur Suche springen
KKeine Bearbeitungszusammenfassung |
|||
| Zeile 1: | Zeile 1: | ||
[[Software:_FEM_-_Tutorial_-_Elektrostatisches_Feld|↑]] <div align="center"> [[Software:_FEM_-_Tutorial_-_Diskretisierung_-_Potentialfeld-Analogien_-_MP|←]] [[Software:_FEM_-_Tutorial_-_Elektrostatik_-_MP_-_Auswertung|→]] </div> | [[Software:_FEM_-_Tutorial_-_Elektrostatisches_Feld|↑]] <div align="center"> [[Software:_FEM_-_Tutorial_-_Diskretisierung_-_Potentialfeld-Analogien_-_MP|←]] [[Software:_FEM_-_Tutorial_-_Elektrostatik_-_MP_-_Auswertung|→]] </div> | ||
<div align="center">''' Modellbildung '''</div> | <div align="center">''' Modellbildung '''</div> | ||
<div align="center">[[Bild:Software_FEMM_-_Elektrostatik_-_Beispiel_leiterplatte.gif]]</div> | |||
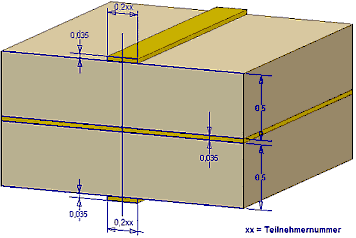
Noch einmal zur Erinnerung der abstrahierte Aufbau des Verdrahtungsträgers: | |||
* Die Kupferschichten sind jeweils 35 µm dick. | |||
* Das Laminat FR4 zwischen Masse-Ebene und Leiterbahnen ist jeweils 0,5 mm dick. | |||
* Die Breite einer Leiterbahn beträgt 0,2xx mm ('''xx'''=01 bis 99). | |||
* FR4-Laminat: ε<sub>r</sub> = 4,7 | |||
Für die Domäne "elektrostatisches Feld" werden folgende Zusammenhänge als bekannt vorausgesetzt: | Für die Domäne "elektrostatisches Feld" werden folgende Zusammenhänge als bekannt vorausgesetzt: | ||
* "Dimensionierungsgleichung" für einen | * "Dimensionierungsgleichung" für einen [http://de.wikipedia.org/wiki/Kondensator_(Elektrotechnik)#Berechnung_der_Kapazit.C3.A4t '''Plattenkondensator'''] bei homogenen Feld: '''C=ε·A/d''' | ||
* "Definitionsgleichung" für die Kapazität: '''C=Q/U''' | * "Definitionsgleichung" für die [http://de.wikipedia.org/wiki/Elektrische_Kapazit%C3%A4t '''elektrische Kapazität''']: '''C=Q/U''' | ||
In dieser Übung wollen wir das erworbene Wissen zur Modellbildung weitestgehend selbstständig anwenden. An dieser Stelle noch einige Hinweise: | In dieser Übung wollen wir das erworbene Wissen zur Modellbildung weitestgehend selbstständig anwenden. An dieser Stelle noch einige Hinweise: | ||
Version vom 24. April 2013, 08:26 Uhr
Modellbildung
Noch einmal zur Erinnerung der abstrahierte Aufbau des Verdrahtungsträgers:
- Die Kupferschichten sind jeweils 35 µm dick.
- Das Laminat FR4 zwischen Masse-Ebene und Leiterbahnen ist jeweils 0,5 mm dick.
- Die Breite einer Leiterbahn beträgt 0,2xx mm (xx=01 bis 99).
- FR4-Laminat: εr = 4,7
Für die Domäne "elektrostatisches Feld" werden folgende Zusammenhänge als bekannt vorausgesetzt:
- "Dimensionierungsgleichung" für einen Plattenkondensator bei homogenen Feld: C=ε·A/d
- "Definitionsgleichung" für die elektrische Kapazität: C=Q/U
In dieser Übung wollen wir das erworbene Wissen zur Modellbildung weitestgehend selbstständig anwenden. An dieser Stelle noch einige Hinweise:
Idealisierungen
Domäne der Elektrostatik:
- Es wird nur das elektrische Feld in den Isolatoren berechnet. Leiter werden als feldfrei angenommen (als ideal leitend).
- Mittels geometrischer Objekte beschreibt man nur den betrachteten Raum für die Isolatoren (Luft/Laminat).
- Grenzen zwischen Isolator und Leiter werden mit dem Leiter-Potential [V] belegt.
- Grenzen zum nicht betrachteten Raum müssen mit geeigneten Randbedingungen versehen werden.
Symmetrie-Eigenschaften:
- Modellieren muss man nur die obere Hälfte der Leiterplatte (Kapazität zwischen Leiterzug und Masseebene).
- Geoemtrie und Feld sind symmetrisch zur Leiterzug-Mitte. Es genügt das Netz z.B. der rechten Hälfte für die Berechnung des elektrischen Feldes.
Grenzenlose Felder:
- Die Kapazität zwischen Leiterbahn und Masse-Ebene wird durch das gesamte elektrostatische Feld bestimmt. Dieses erstreckt sich theoretisch durch den unendlichen Raum. Praktisch genügt der Raum in der Nähe des Leiters.
- Die Breite des Bereiches neben der Leiterbahn sollte mindestens so groß sein wie der Abstand=0,5 mm des Leiters zur Masse-Ebene. Wir verwenden Faktor 10 (Breite=5 mm).
- In geringerem Maße trägt auch das Feld über dem Leiter (durch die Luft) mit zur Kapazität bei. Dieser Luftraum muss deshalb im Modell berücksichtigt werden. Als Höhe des zu vernetzenden Rechtecks wählen wir den Wert der halben Rechteck-Breite (Höhe=2,5 mm).
- Wir verwenden 2D-Elemente. Günstig ist für die Elemente die Dicke=1 m, dann erhält man die berechnete Kapazität sofort als Kapazitätsbelag pro Meter. Die "Dicke" entspricht im Modell der betrachteten Leiterzuglänge.
...